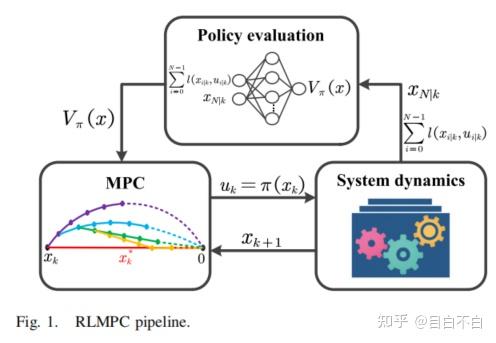
本文所做的代码是基于“Reinforcement Learning-Based Model Predictive Control for Discrete-Time Systems”,发布于IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS, VOL. 35, NO. 3, MARCH 2024。
仅为个人复现,水平有限,如果有差错,,敬请见谅。
代码复现开源地址:基于 lmcggg/RL 的 MPC-for-dts
下面是讲解:
该论文的核心思想在于将MPC和RL通过策略迭代(Policy Iteration, PI)的框架有机地结合起来。在PI框架中,通常包含两个交替进行的步骤:策略评估和策略改进。
- MPC作为策略生成器 (Policy Generator for Improvement): 在RLMPC框架中,MPC扮演了策略生成器的角色。具体而言,在每个控制周期,MPC在线求解一个有限时域优化问题,以产生当前的控制输入。这个优化问题的目标函数由两部分组成:未来N步的累积阶段代价和一个终端代价函数。
- RL用于策略评估 (Policy Evaluation via Value Function Learning): 强化学习技术,特别是价值函数近似(Value Function Approximation, VFA),被用来学习和评估当前MPC生成的策略。具体地,当前策略下系统的长期累积代价(即价值函数
V_π(x)) 被学习出来。这个学到的价值函数随后被用作下一轮MPC优化问题中的终端代价函数。
通过这种方式,形成了一个闭环的迭代过程: 当前策略评估: 利用RL技术(如时序差分学习 Temporal Difference, TD)和VFA(例如,使用参数化的函数如多项式基函数 V_π(x) ≈ W^T Φ(x))学习当前MPC策略(由当前的终端代价 W 定义)的价值函数,得到更新的权重 W'。 策略改进: 将新学到的价值函数 V_π'(x) = W'^T Φ(x) 作为MPC的终端代价函数,MPC通过求解优化问题生成一个改进的控制策略。
论文指出,这种迭代方式使得终端代价函数无需复杂的离线设计,而是通过在线学习得到,并能逐步逼近最优价值函数,从而提升MPC的性能,使其更接近无限时域最优控制的效果。
关键方法与技术细节
- RLMPC优化问题 (OP 2 in paper): 在任意状态
x_k,RLMPC求解如下优化问题:min_{u_k} Σ_{i=0}^{N-1} l(x_{i|k}, u_{i|k}) + V_π(x_{N|k})其中:
l(x, u)是阶段代价函数。N是预测时域。x_{i|k}和u_{i|k}是从当前状态x_k开始预测的未来状态和输入。V_π(x_{N|k})是在预测时域末端状态x_{N|k}处的价值函数,由RL学习得到,形式为W^T Φ(x_{N|k})。
- 价值函数学习 (基于TD学习的参数更新): 论文采用了一种类TD学习的方法来更新价值函数的权重
W。具体步骤如下:
- 数据生成: 对于一系列采样状态
x_j,使用当前MPC策略(即以当前W作为终端代价的MPC)求解得到最优控制序列u_j*和对应的状态轨迹及阶段代价。 - 目标值计算 (J'): 计算这些采样状态下的“真实”累积回报
J'(x_j, u_j*) = Σ_{i=0}^{N-1} l(x_{i|j}, u_{i|j}^*) + W^T Φ(x_{N|j}^*)。注意,这里的终端项W^T Φ(x_{N|j}^*)仍然使用当前的权重W。 - 权重更新 (SGD-like): 使用梯度下降法来最小化目标值
J'和当前价值函数估计W^T Φ(x_j)之间的误差。例如,对于每个样本x_j,更新规则类似于:W ← W + α * [J'(x_j, u_j*) - W^T Φ(x_j)] * Φ(x_j)其中α是学习率。论文的实现细节可能采用批处理更新。
- 理论分析: 论文对所提出的RLMPC框架进行了严格的理论分析,包括:
- 收敛性: 证明了在PI迭代下,价值函数
V_π(x)单调非减地收敛到最优价值函数V*(x)。 - 可行性: 证明了在每次迭代中,MPC优化问题都是递归可行的。
- 稳定性: 证明了闭环系统在每次迭代的策略下都是渐近稳定的。一个关键的洞察是,将RLMPC的迭代过程与一个等效的、预测时域不断累积的MPCWTC(无终端代价MPC)联系起来,从而利用MPCWTC的稳定性理论。
- 优势与特点:
- 无需离线设计终端约束: 消除了传统MPC中设计终端代价、终端约束集和辅助控制器的复杂性。
- 灵活性: 由于终端约束的消除,预测时域的选择更加灵活,有潜力减少计算负担。
- 性能提升: 通过学习终端代价,补偿了截断预测时域带来的次优性,有望达到接近无限时域最优的性能。
- 安全性保障: 即使在价值函数尚未完全学好的情况下,MPC的约束处理能力也能保证系统的运行安全(满足状态和输入约束)。理论分析也保证了学习过程中每一步策略的稳定性。
仿真验证
论文通过线性和非线性(非完整约束车辆)系统的仿真案例,验证了RLMPC框架的有效性。 线性系统: RLMPC能够达到与精心设计的传统LQR(其MPC形式)几乎相同的性能。 非线性系统: RLMPC表现出优于传统MPC(尤其是在终端约束设计困难或保守的情况下)的性能。 (文章中的迭代次数只有十几次,但我的次数是高于他很多,参数方面我已经足够激进,但还是无法得到相同结果,可能是我的q-learn部分设计不好,需要一定的优化,文章中有列出它用的其他的库,但我是自己写,没按这个来。)
具体的结果如下所示:(非线性)

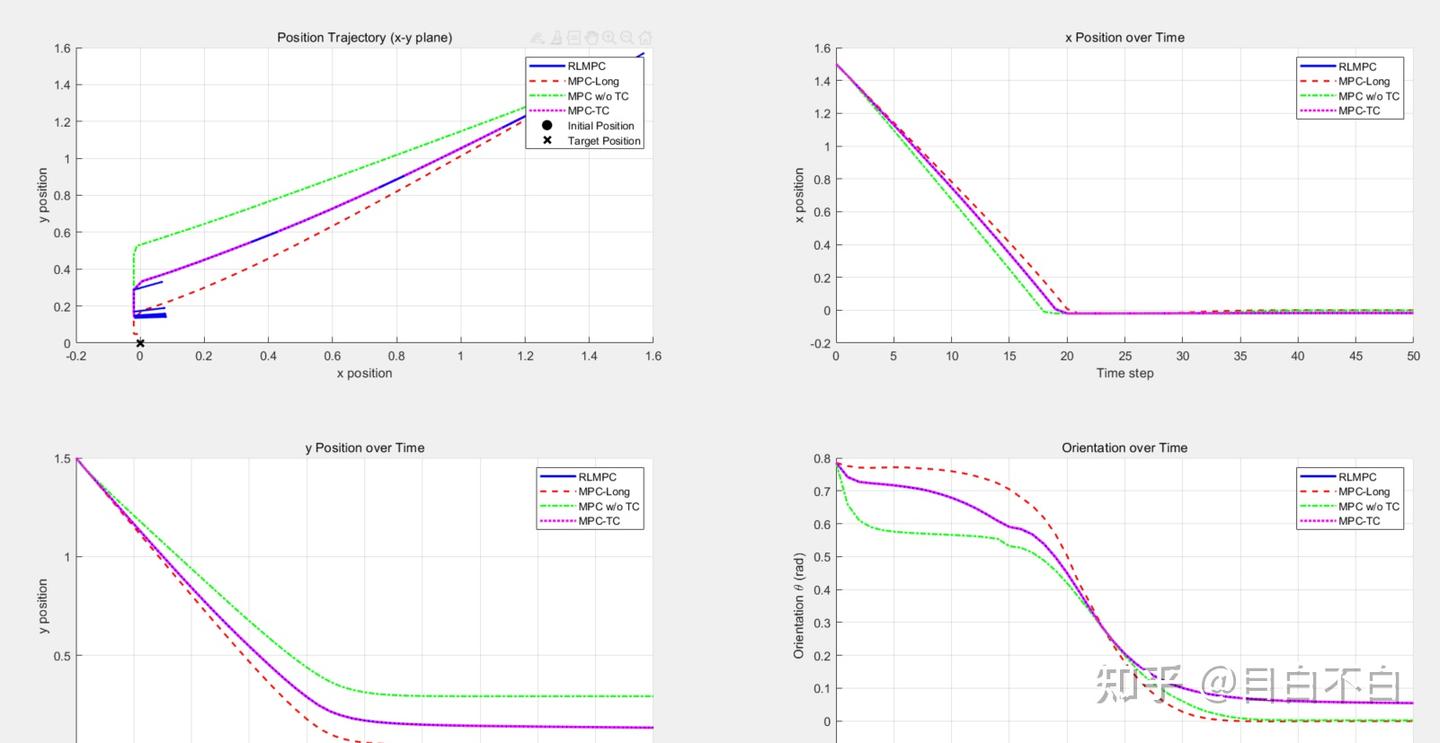
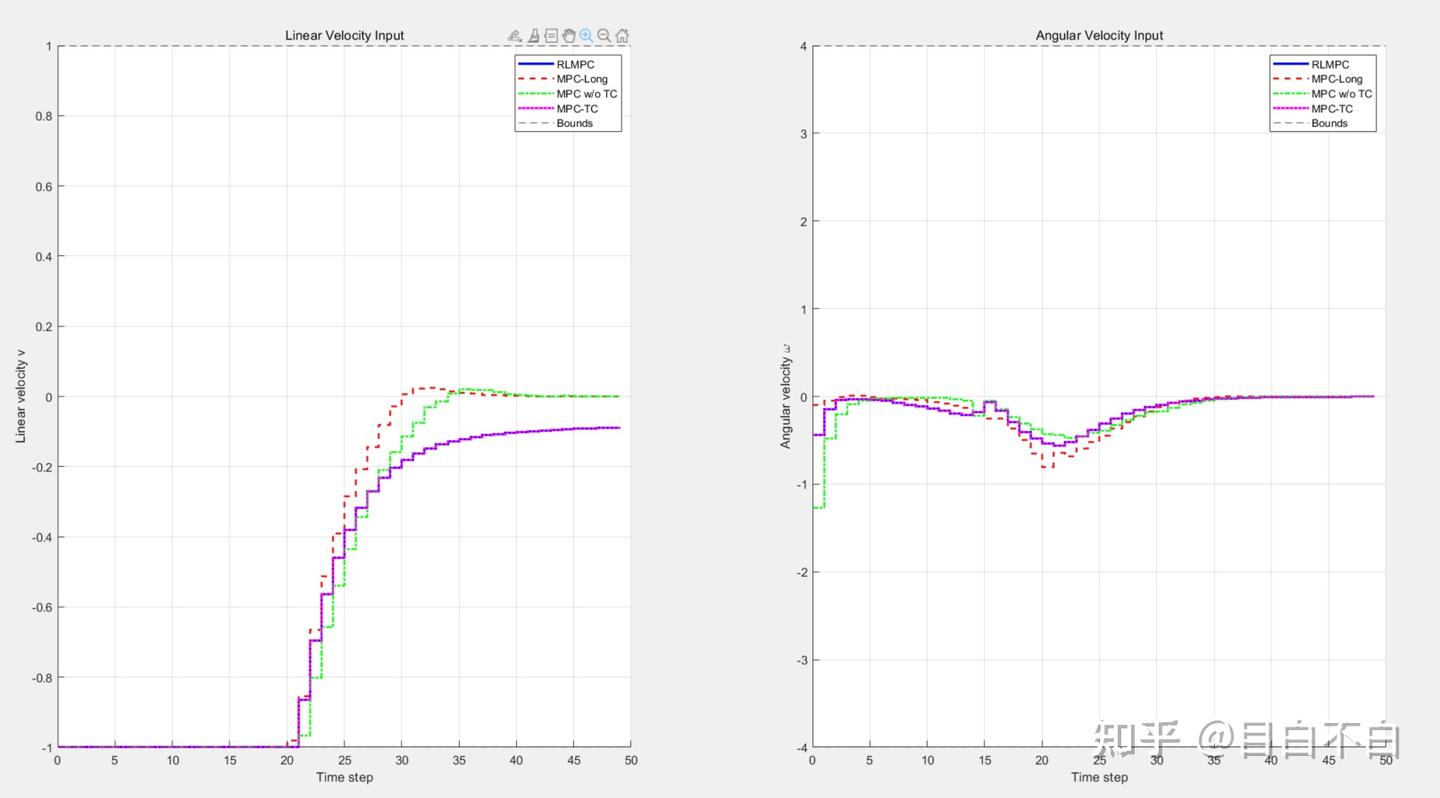
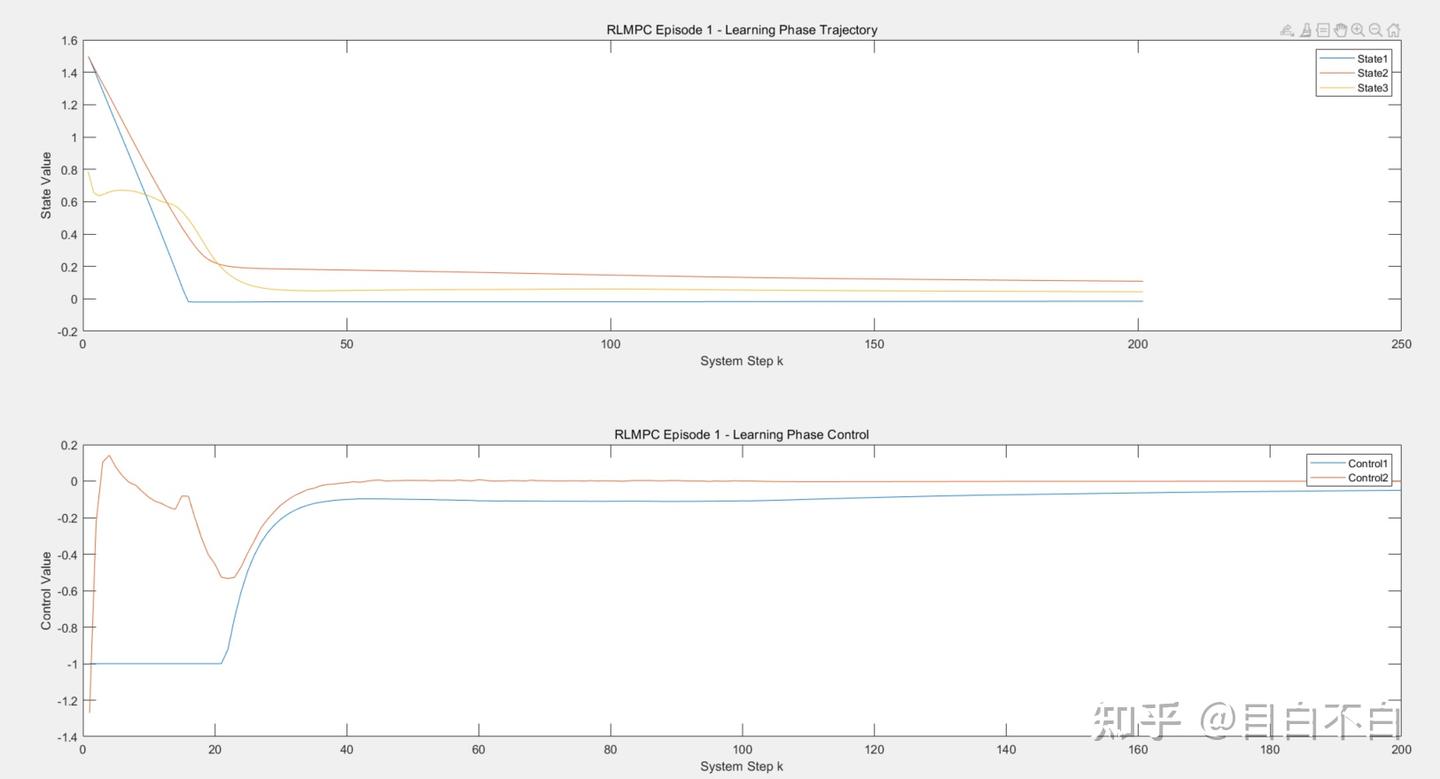
RLMPC Total Cost: 38.3546
MPC-Long Total Cost: 37.7445
MPC w/o TC Total Cost: 41.2104
MPC-TC Total Cost: 38.3546
RLMPC vs MPC-Long improvement: -1.6164%
RLMPC vs MPC w/o TC improvement: 6.9299%
RLMPC vs MPC-TC improvement: 0%
MPC-TC vs MPC w/o TC improvement: 6.9299%
可以看到,该方法的效果和我设计了终端函数的方法几乎是一样的效果。也就是说,在更复杂的任务中,如果我们难以入手进行终端的设计,就可以使用该方法进行自适应设计。